Basic

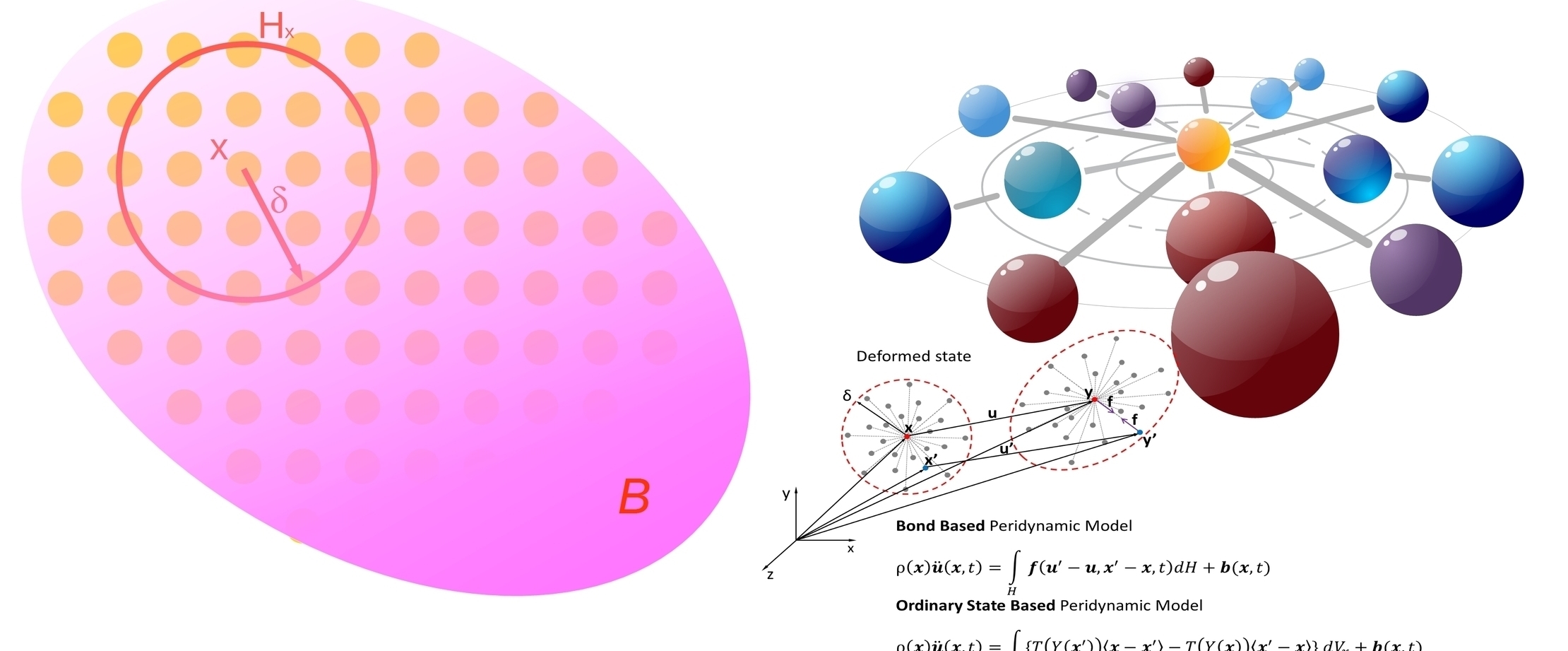
The classical molecular dynamics depends on the locality of material points. In peridynamics theory, each material points is identified by is coordinates x_k and is associated with its incremental volume V_k and the mass density ρ(x_k). Each material point may also be subjected to load, displacement, and velocity which lead to motion and deformation. In a deformaed state, a material point, x_k, experiences a displacement, u_k, and its location is described by its position vector, y_k. The displacement and body load vector are represented as u_k(x_k, t) and b_k(x_k, t).

In the peridynamics theory, the interactions of the material point x_k with the others is assumed to vanish beyond a local range, δ, called horizon. The material points within the distance δ is called the family of x_k, denoted as H_xk. In the other word, it is assumed that a material point only interacts with it own family. The interactions between material points are prescribed as the micropotential that depends on the deformation and the constitutive properties of the material.

Deformation

The deformation of a material point, x_k is influenced by the collective deformations of the other points. In a deformed state, the relative position vector, (x_k - x_j) prior to deformation became (y_k - y_j) after deformation. The stretch between two points x_k and x_j is defined as:
$s$_(k)(j) = (|y_(j) - y_(k)| - |x_(j) - x_(k)|)(|x_(j) - x_(k)|)

The displacement vectors of a material point x_(k) can be stored in a vector:
Y(x_(k), t) =

Force Density

The collective deformation of H_x(k) resulting in a force density vector t_(k)(j) applied on the material point x_(k). Similar to the displacement vectors, the force density vectors of a material point x_(k) can also be stored in an array, T:
T(x_(k), t) = {t_(k)(1), t_(k)(2), …, t_(k)(n)}